2015考研高數:極限計算常用7種突圍方法
[摘要] 極限的計算到底有哪些常用的方法?小編在這里為考生們總結了四則運算法則、洛必達法則、利用泰勒公式求極限 冪指函數的極限計算方法、夾逼定理等七種極限計算突圍方法,希望能給你帶來幫助。
計算極限的常用方法 (一) 四則運算法則 四則運算法則在極限中最直接的應用就是分解,即將復雜的函數分解為若干個相對簡單的函數和、積和商,各自求出極限即可得到要求的極限。但是在分解的時候要注意:(1)分解的各部分各自的極限都要存在;(2)滿足相應四則運算法則,(分母不能為0)。四則運算的另外一個應用就是“抓大頭”。如果極限式中有幾項均是無窮大,就從無窮大中選取起主要作用的那一項,選取的標準是選趨近于無窮最快的那一項,對數函數趨于無窮的速度遠遠小于冪函數,冪函數趨于無窮的速度遠遠小于指數函數。 (二) 洛必達法則(結合等價無窮小替換、變限積分求導) 洛必達法則解決的是“零比零”或“無窮比無窮”型的未定式的形式,所以只要是這兩種形式的未定式都可以考慮用洛必達法則。當然,在用洛必達的時候需要注意(1)它的三個條件都要滿足,尤其要注意第二三個條件,當三個條件都滿足的時候才能用洛必達法則;(2)用洛必達法則之前一定要先化簡,把要求極限的式子化成“干凈”的式子,否則會遇到越求導越麻煩的情況,有的甚至求不出來,所以一定要先化簡。化簡常用的方法就是等價無窮小替換,有時也會用到四則運算。考生一定要熟記常用的等價無窮小,以及替換原則(乘除因子可以替換,加減不要替換)。考研中,除了也常常會把變限積分和洛必達相結合進行考查,這種類型的題目,首先要考慮洛必達,但是我們也要掌握變限積分求導。 另外,考試中有時候不直接考查“零比零”或“無窮比無窮”型,會出“零乘以無窮”,“無窮減無窮”這種形式,我們用的方法就是把他們變成“零比零”或“無窮比無窮”型。 (三) 利用泰勒公式求極限 利用泰勒公式求極限,也是考研中常見的方法。泰勒公式可以將常用的等價無窮小進行推廣,如 (四) 冪指函數的極限計算方法 冪指函數指的是,底數和指數都是函數的函數。對于冪指函數考研中經常考的題型是未定式的形式,如: (五) 夾逼定理 夾逼定理是極限這部分兩個收斂準則之一,數一數二要求掌握并會用它求極限。數三要求了解極限存在的收斂準則,經常以求n項和的極限這種形式出現或數列極限的形式出現。使用夾逼定理的核心在于放縮,即將要計算極限的函數或數列放大和縮小之后分別求極限,如果這兩者的極限都等于同一個數,那么原先的函數或數列的極限也就等于這個數。這里在放縮的時候一般要遵循兩個基本原則:一是要便于計算,二是要適度(也即放縮之后的極限必須一致)。夾逼定理主要用來求數列極限,對數一數二的要求高一些。 (六) 單調有界定理 單調有界定理是極限存在的另一個收斂準則。考研中的題型主要是證明一個數列極限存在,并求其極限常見于數一二,尤其是數二,11、12、13年連續三年考單調有界定理。這種類型題目,主要就是證明數列單調有界(單調遞增有上界,單調遞減有下界)即可。 (七) 定積分定義 考研中求n項和的極限這類題型用夾逼定理做不出來,這時候需要用定積分定義去求極限。常用的是這種形式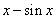 ,
,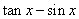 等。也可以用來求解未知極限式中的未知參數,和解決抽象函數的極限。尤其是未知極限式中的未知參數,比起洛必達更適合用泰勒公式去做。
等。也可以用來求解未知極限式中的未知參數,和解決抽象函數的極限。尤其是未知極限式中的未知參數,比起洛必達更適合用泰勒公式去做。 ,
, ,
, 。統一的處理方式是做
。統一的處理方式是做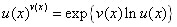 恒等變形,從而只要能計算出極
恒等變形,從而只要能計算出極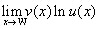 就可以了。當然對于
就可以了。當然對于 的形式除了用剛才那種方法,也可以用重要極限去做。對于
的形式除了用剛才那種方法,也可以用重要極限去做。對于 用兩種方法得出的結果都是
用兩種方法得出的結果都是 ,其中
,其中 。把這個當結論記住,遇到
。把這個當結論記住,遇到 的形式直接用就可以了。
的形式直接用就可以了。 ,只要把要求的極限湊成等是左邊的形式,就可以用定積分去求極限了。
,只要把要求的極限湊成等是左邊的形式,就可以用定積分去求極限了。






