在考研數學中,線性代數是考各類數學的共同考試內容,包括:數學(一)、數學(二)和數學(三),并且在這三類的數學試卷中,線性代數的考題基本相同,所占分值也是一樣的,其難度一般介于高等數學和概率統計之間。線性代數的考試內容劃分為六個方面,包括:行列式、矩陣、向量、線性方程組、特征值與特征向量、二次型。從歷年的考研真題來看,每個方面的考題具有一定的特點和一定的規律,為了幫助廣大考生了解這些特點和規律,小編對其進行了細致的分析總結,供各位考生參考,希望對大家有所幫助。
在《2015考研數學線性代數典型題型分析:行列式(1)》中,向大家介紹了行列式的兩種典型考題,即計算不超過4階的行列式和計算矩陣行列式,在下面將向大家介紹行列式的另一種典型考題——計算n階行列式。首先我們回顧一下行列式的考題特點和常用計算方法。
行列式考題特點:
從歷年考研真題分析看,行列式單獨出題考得不多,常常是與矩陣、線性方程組或特征值的計算結合在一起考。題型常見的通常有三種:一種是計算一個不超過4階的普通行列式,另一種是計算一個矩陣的行列式,還有一種是計算一個比較特殊的n階行列式,通常這個n階行列式可以利用行列式性質或遞推法計算。
行列式的計算方法:
1)利用行列式性質計算;
2)利用遞推法或歸納法計算;
3)利用矩陣行列式性質計算;
4)其它方法,如:增階法,拆項法,定義法。
典型例題分析:
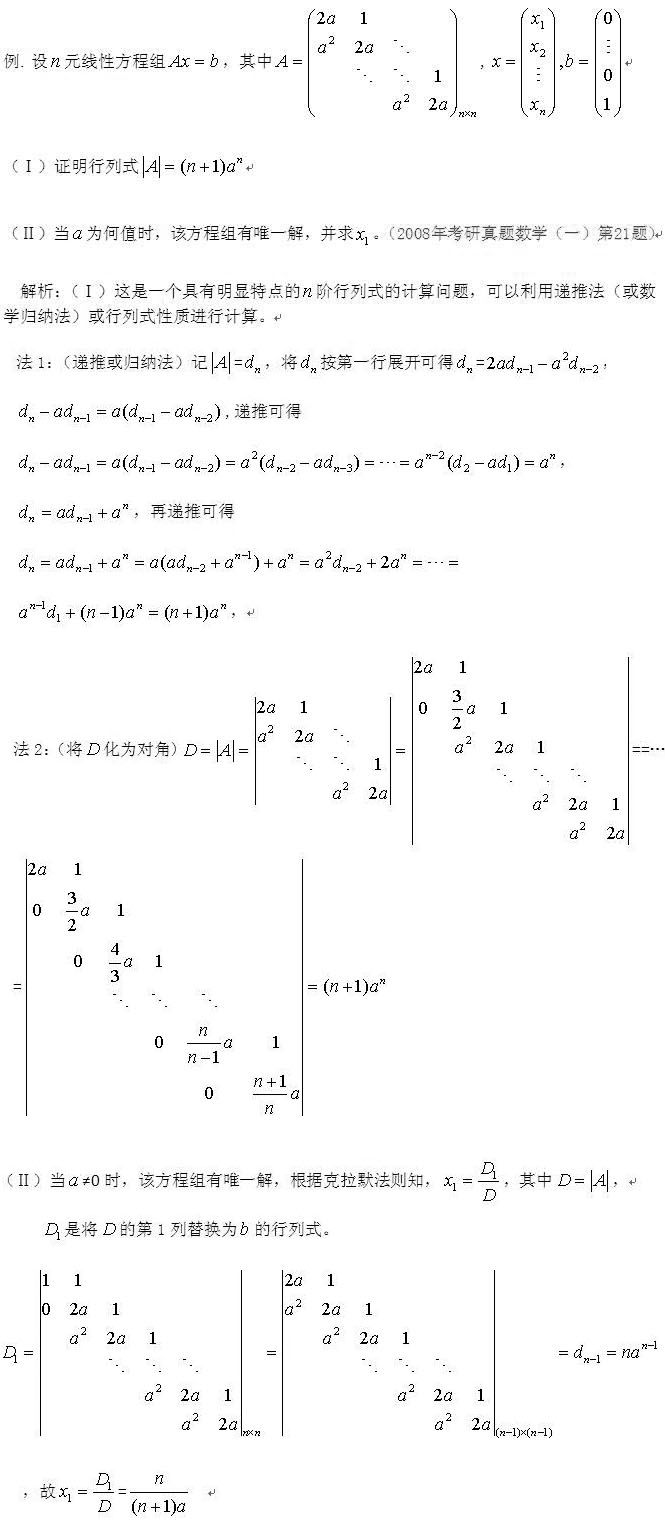
上面就是對考研數學中線性代數部分的行列式有關考點及典型題型的分析,到此為止,我們共向大家介紹了行列式方面的三種典型題類:計算不超過4階的行列式、計算矩陣行列式和關于n階行列式的計算,在以后的時間里,我們還會陸續向大家介紹線性代數其它部分的典型考題分析,希望各位考生留意查看。最后預祝各位學子在2015考研中取得佳績,成功實現自己的人生夢想。